新學制實施在即，對小學教學有何影響呢？大家可以說影響不大，因為新學制只涉及高中；然而連串的教改與課改，已為整個數學教育帶來悄悄變化。首先，一條龍的想法把固有分家的中小學課程連貫起來。小學數學正正要為初中與高中奠定堅實的基礎。此外，中小學的課程發展自20世紀60年代新數學時期，以至千禧年的新課程都是要為學生制訂適切的學習內容，包括減省繁複計算，處理「繁、難、多、舊」，日常生活數學，適當引入現代計算工具等。其中着重促成理解的學習（learning with understanding）、概念性理解（conceptual understanding）、學習興趣和高層次能力。這正配合國際上之數學課程改革，重視資訊科技教學、高層次思維能力、道德價值、一般共通能力、生活數學、專題研習、愉快學習、態度及個別差異等。

　　學生着重探索令課堂變得互動，教師亦得自我裝備，以隨時回應學生的提問。這包含了數學內容知識、一般教學知識及教學內容知識三個範疇。事實上，基礎教育階段的數學一點並不「小兒科」。以數字的認識為例，最初由數數開始，在那個階段，數字是具體實物，到高中認識實數已是一種抽象的「人造物」了，中間需要為學生對數字的認識進行轉型，其中就是透過數線。實數雖然是高中的課題，但數線在小學引入了，中間（以前是高小，現在是初中）引入負數亦是透過數線。

　　數線的引入就大有學問。現時流行用一些卡通人物在數線上行走以加深理解。這未嘗非一種學習之法，其實屬於一般教學知識；換言之，與數學內容沒有直接關係。以負負得正為例，於是老師就要真正理解其學科知識（見附錄1），不過這太深奧了，學生很難明白，於是最好能找得學生接受又帶有數學味道的解說，這就可能是教學內容知識了。例如神忠男便借助槓桿想法把負數看成將數線按原點反影，反影兩次回復原狀，於是負負得正。當然對於高中學生，若真想給予嚴格證明，還應給他看到其中的思路（見附錄2），否則流於死記硬背，由抽象到抽象。

　　有些學生的提問比比皆是。例如廣州的一位同工便曾收到小學生提問：「點沒有大小，為甚麽由點構成的線具有長度？」翻查《幾何原本》，第一卷幾何基礎中用公設1確立了點與線的關係，即「過兩點能作且只能作一直線」，又進一步得出推論「兩條直線相交有且只有一個公共點」，除此沒有其他點與線的關係。現代數學發展了點與線的關係，把線看成是點的集合，從數學教學的角度形象地闡述為「點連續運動形成線」，但是對「連續」缺乏界定，這些問題暴露了數學自身的缺陷，也導致了三次數學危機。到第三次數學危機和希爾伯特重新整理歐幾里得的設基系統前，「連續統」（線段）的「內部構造」仍不很清楚。我們甚至不知道線的中間是否有「隙縫」。如此種種，都是教師須具備的數學內容知識。

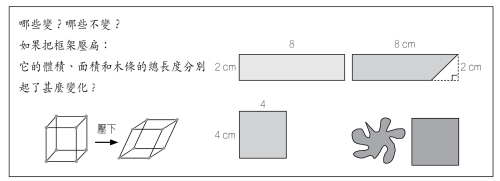圖1 變與不變

　　香港也有中學老師收到類似的問題：「學生問，何以同等周界的長方形和平行四邊形的面積會不一樣。平行四邊形的面積小了些，跑到哪裏去了？」筆者曾為之解答，詳見〈變與不變──面積逃到哪裏去了？〉一文，於此不贅。而其實小學已有涉及這類探索。我們在設計變式課程時，其中一種就是讓學生考察變與不變的關係，從變中得出不變的通則（圖1）。

　　當然，無論對於小學、初中或高中，問題解決均是數學教育之核心。筆者一向認為除了非常規題（如奧數類型題目，這類題目當然有其作用）外，日常習題於發展學生問題解決能力中仍大有可為。

　　最近筆者與一些小學生探討他們解決一些日常小測數學題的方法，例如他們感到比較難做的一題：

「一瓶果汁，天慧喝去半瓶後再加入 150 毫升，現有果汁 600 毫升，這瓶果汁原有多少毫升？」

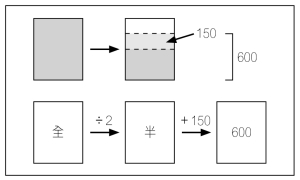圖2 關係圖

　　我們可以透過畫圖去協助思考（圖2）。我們在發展變式課程時也提過可以配合這些關係圖作題型分析，讓學生看到題型的變化（圖3）。這裏我們想提出重點不只是得出幾種標題的題型，而是讓學生看到題目與題目間之關係（關係性理解）。這也是數學學習上自小學到高中的一種一條龍式的學習。

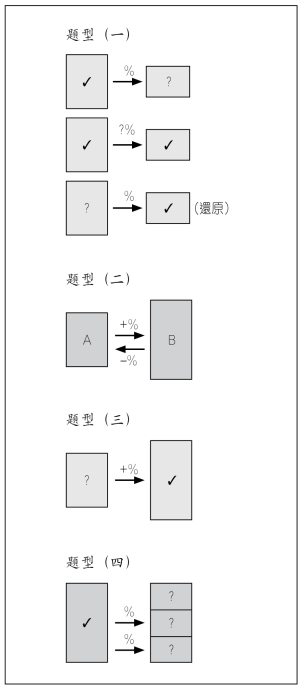圖3 題型分析〔來源：黃毅英、林智中、孫旭花（2006），頁39。〕

附錄1

負負得正

設 k 為 1 的加法逆元。首先證明 0 為「零化子」：0 (a) = (1 – 1)a = a – a = 0

今，1 + k = 0。

0 = (1 + k)k = k + kk

1 = 1 + (k + kk) = (1 + k) + kk = 0 + kk = kk

故 0 = –1(1 – 1) = –1 + (–1) (–1)，

得 1 = (–1) (–1)。

附錄2

思路

※壓抑常識性判斷

※能用的東西只有：

　– 交換律、結合律、分配律

　– 0 是「零化子」

　– 1 + k = 0

　– 可作加法移項

　– 不必考慮除法

※先不考慮 2, 3, ...，故只考慮 0, 1, k

※它們僅有的關係是

　　1 + k = 0

　– 移項：

　　1 + k + 1 = 1

　　　 1 + 0 = 1

　　沒意思

　– 從零化子着手

　　(a) 0·1 = 0 無意思

　　(b) 　　　0·k = 0

　　　 　(1 + k)k = 0

　　　　　k + k·k = 0

　　　　抽它出來時要移走前面的 k：

　　　1 + k + k·k = 1

　　　　　　k·k = 1

參考資料
	感謝中文大學教育學院之學員提供部分實際事例。
	鄧國俊、黃毅英、霍秉坤、顏明仁、黃家樂（2006），《香港近半世紀漫漫「小學數教路」：現代化、本土化、普及化、規範化與專業化》。香港：香港數學教育學會。
	李柏良（2004），〈香港數學課程發展：由現況探討未來〉，載鄧幹明、黃家樂、李文生、莫雅慈（編）《香港數學教育會議 ── 2004 論文集》。香港：香港數學教育學會。
	Kwan, G. S. K. (2003)，Highlights of the new mathematics curriculum in Hong Kong，載鄧幹明、曾倫尊（編）《學會學習：數學課程改革評析》（頁28—36）。香港：香港數學教育學會。
	Wong, N. Y., Han, J. W., & Lee, P. Y. (2004). The Mathematics Curriculum: Towards Globalisation or Westernisation? In L. Fan, N. Y. Wong, J. Cai, & S. Li (Eds.), How Chinese learn mathematics: Perspectives from insiders (pp. 27-70). Singapore: World Scientific. 中譯：黃毅英、韓繼偉、李秉彝（2005），〈數學課程：趨向全球化還是趨向西方化〉，載於范良火、黃毅英、蔡金法、李士錡（編）《華人如何學習數學》（頁24—61）。南京：江蘇教育出版社。
	黃毅英、許世紅（2009），〈數學教學內容知識:結構特徵與研發舉例〉，《數學教育學報》18卷1期，5—9。
	張家麟、黃毅英、韓藝詩（2009），《新高中數學學習領域的教學（必修部分）》。香港：課程發展處數學教育組。
	黃毅英（2003），〈從認識論的課程分析看現行中小學課程的幾個問題〉，載鄧幹明、曾倫尊（編）《學會學習：數學課程改革評析》（頁3—24）。香港：香港數學教育學會。 黃毅英（2007），〈三次數學危機 ── 個人認知與體會〉，《中學數學教學研究》。2/2007，7—10。
	Siu, F. K., & Siu, M. K. (1992). Why is (–) × (–) = (+) ?. Curriculum Forum, 2(2), 47 – 51.
	神忠男（2002），《愛麗絲與孫悟空的數學之旅》。臺北：國際村文庫書店。
	許世紅、黃毅英（待刊），〈研發數學教學內容知識，提高教師培訓效益〉。
	黃毅英（待刊），〈變與不變 ── 面積逃到那裏去了？〉，《香港數理教育學會會刊》25期。
	其中研究得到現代教育研究社資助，謹此鳴謝。
	黃毅英、林智中、孫旭花（2006），《變式教學課程設計原理：數學課程改革的可能出路》。香港：香港中文大學教育學院香港教育研究所。
	National Council of Supervisors of Mathematics. (1977). Position paper on basic mathematical skills. Washington, DC: National Institute of Education.
	Wong, N. Y. (1994). Enhancing students’ mathematics problem solving ability in day-to-day teaching. Curriculum Forum, 3(3), 24 – 33.
	黃毅英（2007），〈數學化過程與數學理解〉，《數學教育》25期，2—18。