|
前文提要 |
在本文的第一部分中,筆者介紹了拉希模型,並提供了該模型的公式
其中 p 為一個學生能成功答對一條題目的概率
B 為該學生的能力值
D 為該題目的難度值
而 B 及
D 皆為正數。
在本文的第二部分中,筆者用一個小測驗,說明了各題的難度值和各考生的能力值是怎樣計算出來的。 |
怎樣計算題庫新增題目的難度值
當試題庫加入了新題目後,負責管理題庫的分析員必須為那些新題目,以固有的準則,來計算它們的難度值。本部分將在這方面有詳細的介紹,並舉例說明執行的方法。
假設,我們的試題庫已有五條舊題目,其難度值經已在同文第二部分計算好(見第二部分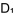 , ,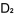 , ,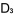 , ,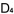 , ,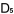 之值)〔原文載於第84期同文之(二)〕。現在有三條新題目須加入題庫,我們應該怎樣計算它們的難度值呢? 之值)〔原文載於第84期同文之(二)〕。現在有三條新題目須加入題庫,我們應該怎樣計算它們的難度值呢?
為了計算新題目的難度值,第一個步驟就是用這些新題目和一些舊題目共同組成一張試卷,然後向一組學生施測,把收集了的數據利用第二部分所介紹的方法進行分析計算。(通常,我們會把數據輸入電腦,然後用既定的電腦程式(program)來作分析計算。)
作為一個實際的例子,我們取舊題目Q3,Q4,Q5(難度值已知,它們分別為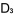 , ,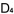 , ,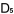 )與新題目
Q6,Q7,Q8
共同組成一份試卷。在分析中,我們用6個新的未知數 )與新題目
Q6,Q7,Q8
共同組成一份試卷。在分析中,我們用6個新的未知數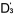 , ,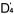 , ,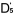 , ,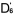 , ,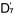 , ,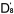 來
表示這六條題目的難度值。在計算的過程中,會到達下面的方程。 來
表示這六條題目的難度值。在計算的過程中,會到達下面的方程。
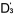 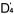 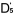 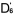 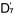 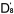 = k …………(21)
= k …………(21)
其中 k 為一個待定常數。
在這方程中,我們依照慣常的做法取 k = 1,則可得到 6 個未知數的值(參看表11的第 3 列)。在這個步驟中,我們發現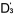 , ,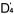 , ,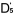 不等於 不等於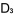 , ,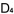 , ,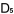 。那麼該怎樣辦呢?是否拉希模型在這裡行不通呢? 。那麼該怎樣辦呢?是否拉希模型在這裡行不通呢?
為了使 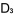 = =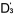 , ,
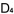 = =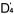 , ,
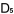 = =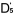 ,我們需要選擇合適的常數
k。k 值的計算有賴以下的比率: ,我們需要選擇合適的常數
k。k 值的計算有賴以下的比率: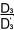 , ,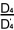 , ,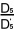 ,這些比率的值分別為
2.97,3.04 和 2.99,它們非常接近。 ,這些比率的值分別為
2.97,3.04 和 2.99,它們非常接近。
初步的觀察告訴我們應當取這 3 個值的平均數為 k 值。但是,這個領域的大部分專家推薦用這些值的幾何平均數(而不是用算術平均數)作為
k 值。因此,
k = 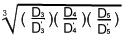
= 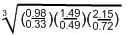
= 2.999
 3.00 3.00
當使用 k = 3(參看表 11 第四列),我們發現題目 Q3,Q4
和 Q5 的難度值與第 2 列所載的難度值非常接近,並且是根據題庫已有的準則,來釐定所有新題目的難度值,包括新題目
Q6,Q7 和 Q8
。所以無論在什麼時候,要向題庫添加新題目時,我們必須用這些步驟,來計算新題目的難度值。
|
第一列
|
第二列
|
第三列
|
第四列
|
|
難度值
題目 |
五條題目的計算 |
六條題目的計算
|
| k=1時的D值 |
k=1時的 值 值 |
k=3時的 值 值 |
|
Q1
|
0.40
|
-
|
-
|
|
Q2
|
0.79
|
-
|
-
|
|
Q3
|
0.98
|
0.33
|
0.99
|
|
Q4
|
1.49
|
0.49
|
1.47
|
|
Q5
|
2.15
|
0.72
|
2.16
|
|
Q6
|
-
|
1.60
|
4.80
|
|
Q7
|
-
|
1.80
|
5.40
|
|
Q8
|
-
|
3.00
|
9.00
|
表11
從這個例子,我們可以看出新計算出來的難度值,只要乘一個適合的常數,便可以作為正確的難度值使用。而這常數的計算,則倚賴那些舊題目在新、舊難度值的差異。
在下一節,我們須要向讀者介紹「難度指數」δ 代替「難度值」D,而二者的關係是
D=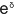 =2.718 =2.718 或 δ=log
或 δ=log D
D
(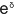 =2.718…,log =2.718…,log 則是以 e 為底的對數)
則是以 e 為底的對數)
用了「難度指數」,有甚麼好處呢?用了「難度指數」,好處多不勝數。k的計算可由幾何平均變為算術平均;新計算出的難度指數只要加一個適當的常數便可適用了。所以,要靈活運用拉希模型,我們要對指數的運算和使用應有相當的了解和認識。
「難度指數」的介紹
以指數形式表示難度值
在第二部分的例子裡,我們介紹了拉希模型,因而為每一條題目設置一個未知數(稱為難度值),及後我們用數學方法,成功地計算出這些未知數。請注意,這樣我們已在拉希模型的運用中,成功地踏出了第一步。但是,我們並沒有使用指數形式來表達,因此,在了解和使用拉希模型時,用指數形式來表達不是必須的。但是,在文獻裡,通常談及拉希模型的文章,都用指數形式來書寫。因此,在本節裡,我們希望讀者能熟悉運用指數表達的形式,以便將來閱讀其他有關拉希模型的文獻。
若用指數來表達,我們用 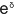 (其中 (其中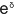 = 2.71828…)取代D的位置,因此 D =
= 2.71828…)取代D的位置,因此 D = 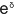 。為了避免在本文中混淆,我們稱
δ 為「難度指數」(而 D 仍然稱為「難度值」)。 。為了避免在本文中混淆,我們稱
δ 為「難度指數」(而 D 仍然稱為「難度值」)。
同樣地,我們用 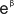 取代學生的「能力值」B,因此 B =
取代學生的「能力值」B,因此 B = 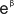 。為了避免混淆,我們稱β為「能力指數」(而
B 仍然稱為「能力值」)。 。為了避免混淆,我們稱β為「能力指數」(而
B 仍然稱為「能力值」)。
在本港中三 / 中四的數學課程裡,學生須要學指數函數(exponential functions)和對數函數(logarithmic
functions)並了解
2 = 10      和 3 = 10
和 3 = 10  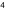 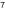 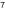  的運作,可把乘法變為加法,例如
的運作,可把乘法變為加法,例如
6 = 2 X 3
= 10      X 10
X 10  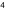 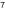 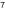 
= 10         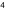 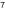 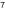 
= 10  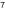 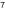  
相信讀者們已慣用以 10 為底的對數,現在的指數表達的形式只是把對數的底的數值,由 10 轉換為 e,e 的值是 2.718…。
若使用指數形式來表達,拉希模型的公式便由
變為
其中 p 為一個學生能成功答對一條題目的概率
β為該學生的能力指數
δ為該題目的難度指數
用了難度指數來表達,表 11 的數值變成 了下面表 12 的數值。
|
第一列
|
第二列
|
第三列
|
第四列
|
|
難度指數
題目 |
五條題目的計算 |
六條題目的計算
|
常數=0時
δ的值(註3) |
常數=0時
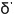 的值(註4) 的值(註4) |
常數=1.10時
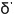 的值(註5) 的值(註5) |
|
Q1
|
-0.92(註1)
|
-
|
-
|
|
Q2
|
-0.23(註2)
|
-
|
-
|
|
Q3
|
-0.02
|
-1.11
|
-0.01
|
|
Q4
|
0.40
|
-0.72
|
0.38
|
|
Q5
|
0.77
|
-0.33
|
0.77
|
|
Q6
|
-
|
0.47
|
1.57
|
|
Q7
|
-
|
0.59
|
1.69
|
|
Q8
|
-
|
1.10
|
2.20
|
表12
註 1:從表 11 中,Q1 的 D = 0.40
因為 0.40 = 2.718     , ,
所以 Q1 的δ= -0.92
註2:從表 11 中,Q2 的 D = 0.79
因為 0.79 = 2.718     , ,
所以 Q2 的δ= -0.23
對於所有在表 11 和表 12 的對應格子的數字,都具有這樣的關係。
註3:在本列的五個數字(-0.92,-0.23, -0.02,0.40,0.77),它們的和是零,它們是由電腦程式計算出來的。這現象正與同文第二部分的方程(21)所說的事情相符。
同文第二部分這樣說
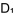 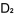 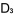 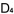 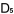 = 1 ……………… (21)
= 1 ……………… (21)
若以指數形式表(21),則把它寫成
e  .e .e  .e .e  .e .e 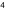 .e .e  = 1 = e
= 1 = e ……… (22) ……… (22)
e          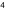    = e
= e …………… (23) …………… (23)
δ1 + δ2 + δ3 +
δ4 + δ5 = 0 …… (24)
註4:在本列的六個數字(-1.11,-0.72, -0.33,0.47,0.59,1.10),它們的和是零,它們是由電腦程式計算出來的。理由已在註
3 說明了。
註5:把第三列的每一個數字加了 1.10 便成為第四列的數字。而第四列的數字正就是我們渴求的新題目的難度指數。 至於為甚麼要加
1.10 呢?它是怎樣計算出來的呢?
它是那三條舊題目(Q3,Q4,Q5)在新、舊指數的平均的差額。我們稱它為調整常數。
調整常數 = 舊題目的舊指數的平均 - 舊題目的新指數的平均
= (-0.02 + 0.40 + 0.77) / 3 -[(-1.11) + (-0.72) + (-0.33)] / 3
= 0.383 -[-0.72]
= 1.1033
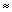 1.10 1.10
其所需的道理也很顯淺,讀者稍加思索,便會明白。
本文在前兩篇旳內容介紹了拉希模型和難度值的計算,好使讀者知道怎樣把題目庫內每一條題目,給予一個難度值。本篇則介紹題目庫加入了新的題目後所須做的跟進工作,這就是必須為每一條新加入的題目,設置一個用同一尺度計算的難度值。本篇亦開始引用「難度指數」,把「難度值」改寫為「難度指數」。在下一篇(最後一篇),本文將向讀者介紹拉希模型題目庫,在水平訂定方面的應用。
(下期待續)
|
參考文件 |
| 1. |
Andrich,D. (1978). A rating formulation for ordered response
categories. Psychometrika, 43, 561-573. |
| 2. |
Masters,G..N. (1982). A Rasch model for partial credit scoring.
Psychometrika, 47, 149-174 |
| 3. |
Rasch,G. (1960). Probabilistic models for some intelligence
and attainment tests. Copenhagen: Danish Institute of Educational
Research. |
| 4. |
Willmott, A. and Fowles, D. The Objective Interpretation
of Test Performance: The Rasch Model Applied. Atlantic Highlands,
N.J.: NFER Publishing Co. Ltd., 1974. |
|